在機(jī)器學(xué)習(xí)領(lǐng)域，有種說法叫做“世上沒有免費(fèi)的午餐”，簡而言之，它是指沒有任何一種算法能在每個(gè)問題上都能有最好的效果，這個(gè)理論在監(jiān)督學(xué)習(xí)方面體現(xiàn)得尤為重要。

舉個(gè)例子來說，你不能說神經(jīng)網(wǎng)絡(luò)永遠(yuǎn)比決策樹好，反之亦然。模型運(yùn)行被許多因素左右，例如數(shù)據(jù)集的大小和結(jié)構(gòu)。

因此，你應(yīng)該根據(jù)你的問題嘗試許多不同的算法，同時(shí)使用數(shù)據(jù)測試集來評估性能并選出最優(yōu)項(xiàng)。

當(dāng)然，你嘗試的算法必須和你的問題相切合，其中的門道便是機(jī)器學(xué)習(xí)的主要任務(wù)。打個(gè)比方，如果你想打掃房子，你可能會(huì)用到吸塵器、掃帚或者拖把，但你肯定不會(huì)拿把鏟子開始挖坑吧。

對于渴望了解機(jī)器學(xué)習(xí)基礎(chǔ)知識(shí)的機(jī)器學(xué)習(xí)新人來說，這兒有份數(shù)據(jù)科學(xué)家使用的十大機(jī)器學(xué)習(xí)算法，為你介紹這十大算法的特性，便于大家更好地理解和應(yīng)用，快來看看吧。

01、線性回歸

線性回歸可能是統(tǒng)計(jì)學(xué)和機(jī)器學(xué)習(xí)中最知名和最易理解的算法之一。

由于預(yù)測建模主要關(guān)注最小化模型的誤差，或者以可解釋性為代價(jià)來做出最準(zhǔn)確的預(yù)測。我們會(huì)從許多不同領(lǐng)域借用、重用和盜用算法，其中涉及一些統(tǒng)計(jì)學(xué)知識(shí)。

線性回歸用一個(gè)等式表示，通過找到輸入變量的特定權(quán)重(B)，來描述輸入變量(x)與輸出變量(y)之間的線性關(guān)系。

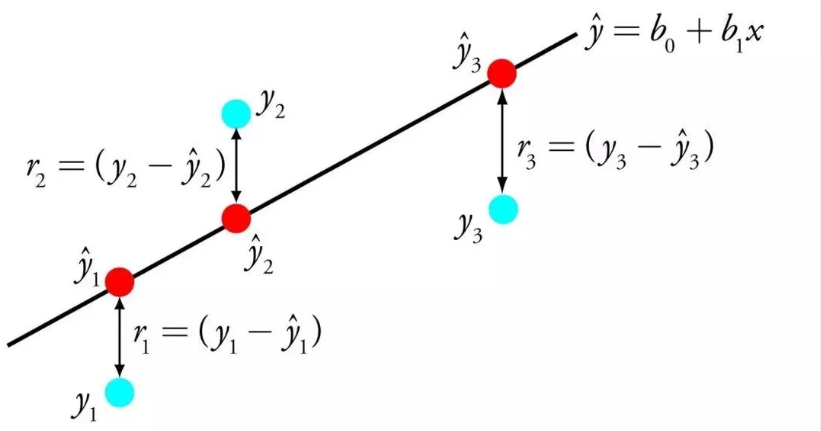
舉例：y = B0 + B1 * x

給定輸入x，我們將預(yù)測y，線性回歸學(xué)習(xí)算法的目標(biāo)是找到系數(shù)B0和B1的值。

可以使用不同的技術(shù)從數(shù)據(jù)中學(xué)習(xí)線性回歸模型，例如用于普通最小二乘和梯度下降優(yōu)化的線性代數(shù)解。

線性回歸已經(jīng)存在了200多年，并且已經(jīng)進(jìn)行了廣泛的研究。如果可能的話，使用這種技術(shù)時(shí)的一些經(jīng)驗(yàn)法則是去除非常相似(相關(guān))的變量并從數(shù)據(jù)中移除噪聲。這是一種快速簡單的技術(shù)和良好的第一種算法。

02、邏輯回歸

邏輯回歸是機(jī)器學(xué)習(xí)從統(tǒng)計(jì)領(lǐng)域借鑒的另一種技術(shù)。這是二分類問題的專用方法(兩個(gè)類值的問題)。

邏輯回歸與線性回歸類似，這是因?yàn)閮烧叩哪繕?biāo)都是找出每個(gè)輸入變量的權(quán)重值。與線性回歸不同的是，輸出的預(yù)測值得使用稱為邏輯函數(shù)的非線性函數(shù)進(jìn)行變換。

邏輯函數(shù)看起來像一個(gè)大S，并能將任何值轉(zhuǎn)換為0到1的范圍內(nèi)。這很有用，因?yàn)槲覀兛梢詫⑾鄳?yīng)規(guī)則應(yīng)用于邏輯函數(shù)的輸出上，把值分類為0和1(例如，如果IF小于0.5，那么 輸出1)并預(yù)測類別值。

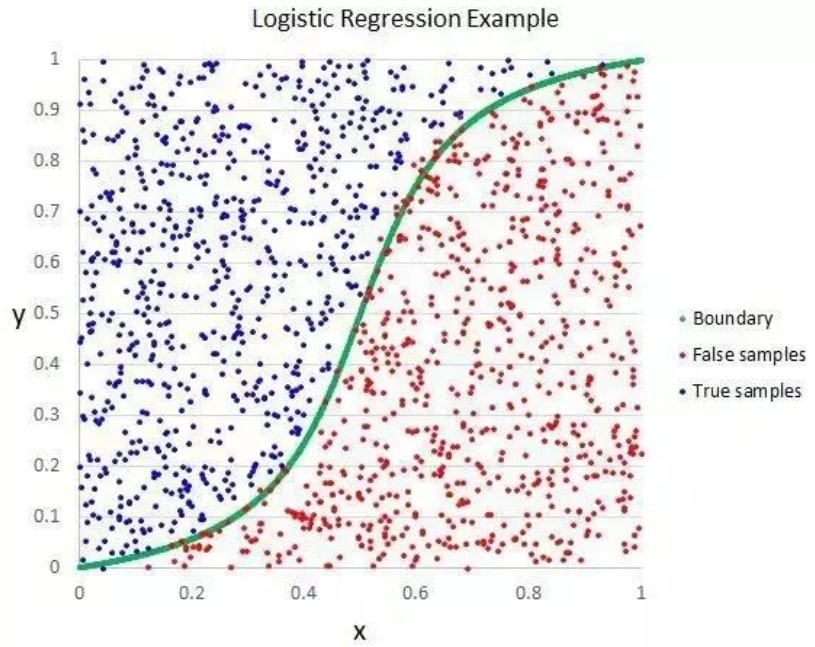
由于模型的特有學(xué)習(xí)方式，通過邏輯回歸所做的預(yù)測也可以用于計(jì)算屬于類0或類1的概率。這對于需要給出許多基本原理的問題十分有用。

與線性回歸一樣，當(dāng)你移除與輸出變量無關(guān)的屬性以及彼此非常相似(相關(guān))的屬性時(shí)，邏輯回歸確實(shí)會(huì)更好。這是一個(gè)快速學(xué)習(xí)和有效處理二元分類問題的模型。

03、線性判別分析

傳統(tǒng)的邏輯回歸僅限于二分類問題。如果你有兩個(gè)以上的類，那么線性判別分析算法(Linear Discriminant Analysis，簡稱LDA)是首選的線性分類技術(shù)。

LDA的表示非常簡單。它由你的數(shù)據(jù)的統(tǒng)計(jì)屬性組成，根據(jù)每個(gè)類別進(jìn)行計(jì)算。對于單個(gè)輸入變量，這包括：

每類的平均值。

跨所有類別計(jì)算的方差。

LDA通過計(jì)算每個(gè)類的判別值并對具有最大值的類進(jìn)行預(yù)測來進(jìn)行。該技術(shù)假定數(shù)據(jù)具有高斯分布(鐘形曲線)，因此最好先手動(dòng)從數(shù)據(jù)中移除異常值。這是分類預(yù)測建模問題中的一種簡單而強(qiáng)大的方法。

04、分類和回歸樹

決策樹是機(jī)器學(xué)習(xí)的一種重要算法。

決策樹模型可用二叉樹表示。對，就是來自算法和數(shù)據(jù)結(jié)構(gòu)的二叉樹，沒什么特別。每個(gè)節(jié)點(diǎn)代表單個(gè)輸入變量(x)和該變量上的左右孩子(假定變量是數(shù)字)。

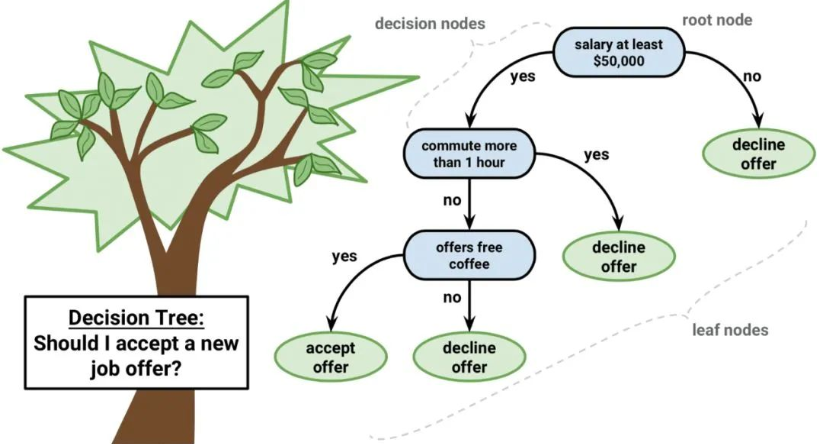
樹的葉節(jié)點(diǎn)包含用于進(jìn)行預(yù)測的輸出變量(y)。預(yù)測是通過遍歷樹進(jìn)行的，當(dāng)達(dá)到某一葉節(jié)點(diǎn)時(shí)停止，并輸出該葉節(jié)點(diǎn)的類值。

決策樹學(xué)習(xí)速度快，預(yù)測速度快。對于許多問題也經(jīng)常預(yù)測準(zhǔn)確，并且你不需要為數(shù)據(jù)做任何特殊準(zhǔn)備。

05、樸素貝葉斯

樸素貝葉斯是一種簡單但極為強(qiáng)大的預(yù)測建模算法。

該模型由兩種類型的概率組成，可以直接從你的訓(xùn)練數(shù)據(jù)中計(jì)算出來：1)每個(gè)類別的概率; 2)給定的每個(gè)x值的類別的條件概率。一旦計(jì)算出來，概率模型就可以用于使用貝葉斯定理對新數(shù)據(jù)進(jìn)行預(yù)測。當(dāng)你的數(shù)據(jù)是數(shù)值時(shí)，通常假設(shè)高斯分布(鐘形曲線)，以便可以輕松估計(jì)這些概率。

樸素貝葉斯被稱為樸素的原因，在于它假設(shè)每個(gè)輸入變量是獨(dú)立的。這是一個(gè)強(qiáng)硬的假設(shè)，對于真實(shí)數(shù)據(jù)來說是不切實(shí)際的，但該技術(shù)對于大范圍內(nèi)的復(fù)雜問題仍非常有效。

06、K近鄰

KNN算法非常簡單而且非常有效。KNN的模型用整個(gè)訓(xùn)練數(shù)據(jù)集表示。是不是特簡單?

通過搜索整個(gè)訓(xùn)練集內(nèi)K個(gè)最相似的實(shí)例(鄰居)，并對這些K個(gè)實(shí)例的輸出變量進(jìn)行匯總，來預(yù)測新的數(shù)據(jù)點(diǎn)。對于回歸問題，新的點(diǎn)可能是平均輸出變量，對于分類問題，新的點(diǎn)可能是眾數(shù)類別值。

成功的訣竅在于如何確定數(shù)據(jù)實(shí)例之間的相似性。如果你的屬性都是相同的比例，最簡單的方法就是使用歐幾里德距離，它可以根據(jù)每個(gè)輸入變量之間的差直接計(jì)算。

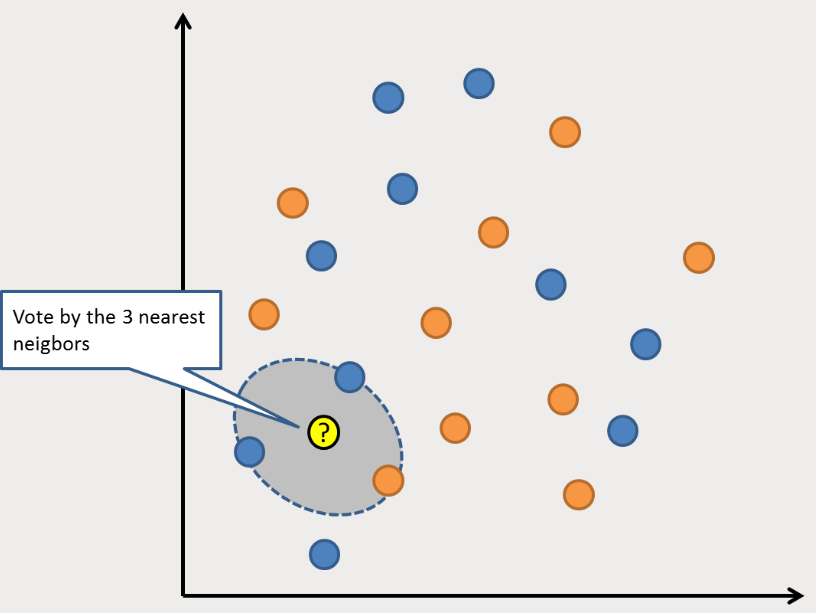
KNN可能需要大量的內(nèi)存或空間來存儲(chǔ)所有的數(shù)據(jù)，但只有在需要預(yù)測時(shí)才會(huì)執(zhí)行計(jì)算(或?qū)W習(xí))。你還可以隨時(shí)更新和管理你的訓(xùn)練集，以保持預(yù)測的準(zhǔn)確性。

距離或緊密度的概念可能會(huì)在高維環(huán)境(大量輸入變量)下崩潰，這會(huì)對算法造成負(fù)面影響。這類事件被稱為維度詛咒。它也暗示了你應(yīng)該只使用那些與預(yù)測輸出變量最相關(guān)的輸入變量。

07、學(xué)習(xí)矢量量化

K-近鄰的缺點(diǎn)是你需要維持整個(gè)訓(xùn)練數(shù)據(jù)集。學(xué)習(xí)矢量量化算法(或簡稱LVQ)是一種人工神經(jīng)網(wǎng)絡(luò)算法，允許你掛起任意個(gè)訓(xùn)練實(shí)例并準(zhǔn)確學(xué)習(xí)他們。

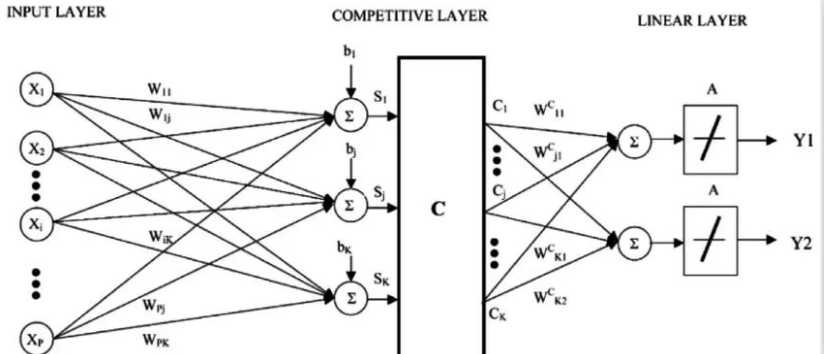
LVQ用codebook向量的集合表示。開始時(shí)隨機(jī)選擇向量，然后多次迭代，適應(yīng)訓(xùn)練數(shù)據(jù)集。在學(xué)習(xí)之后，codebook向量可以像K-近鄰那樣用來預(yù)測。通過計(jì)算每個(gè)codebook向量與新數(shù)據(jù)實(shí)例之間的距離來找到最相似的鄰居(最佳匹配)，然后返回最佳匹配單元的類別值或在回歸情況下的實(shí)際值作為預(yù)測。如果你把數(shù)據(jù)限制在相同范圍(如0到1之間)，則可以獲得最佳結(jié)果。

如果你發(fā)現(xiàn)KNN在您的數(shù)據(jù)集上給出了很好的結(jié)果，請嘗試使用LVQ來減少存儲(chǔ)整個(gè)訓(xùn)練數(shù)據(jù)集的內(nèi)存要求。

08、支持向量機(jī)

支持向量機(jī)也許是最受歡迎和討論的機(jī)器學(xué)習(xí)算法之一。

超平面是分割輸入變量空間的線。在SVM中，會(huì)選出一個(gè)超平面以將輸入變量空間中的點(diǎn)按其類別(0類或1類)進(jìn)行分離。在二維空間中可以將其視為一條線，所有的輸入點(diǎn)都可以被這條線完全分開。SVM學(xué)習(xí)算法就是要找到能讓超平面對類別有最佳分離的系數(shù)。

超平面和最近的數(shù)據(jù)點(diǎn)之間的距離被稱為邊界，有最大邊界的超平面是最佳之選。同時(shí)，只有這些離得近的數(shù)據(jù)點(diǎn)才和超平面的定義和分類器的構(gòu)造有關(guān)，這些點(diǎn)被稱為支持向量，他們支持或定義超平面。在具體實(shí)踐中，我們會(huì)用到優(yōu)化算法來找到能最大化邊界的系數(shù)值。

SVM可能是最強(qiáng)大的即用分類器之一，在你的數(shù)據(jù)集上值得一試。

09、bagging和隨機(jī)森林

隨機(jī)森林是最流行和最強(qiáng)大的機(jī)器學(xué)習(xí)算法之一。它是一種被稱為Bootstrap Aggregation或Bagging的集成機(jī)器學(xué)習(xí)算法。

bootstrap是一種強(qiáng)大的統(tǒng)計(jì)方法，用于從數(shù)據(jù)樣本中估計(jì)某一數(shù)量，例如平均值。它會(huì)抽取大量樣本數(shù)據(jù)，計(jì)算平均值，然后平均所有平均值，以便更準(zhǔn)確地估算真實(shí)平均值。

在bagging中用到了相同的方法，但最常用到的是決策樹，而不是估計(jì)整個(gè)統(tǒng)計(jì)模型。它會(huì)訓(xùn)練數(shù)據(jù)進(jìn)行多重抽樣，然后為每個(gè)數(shù)據(jù)樣本構(gòu)建模型。當(dāng)你需要對新數(shù)據(jù)進(jìn)行預(yù)測時(shí)，每個(gè)模型都會(huì)進(jìn)行預(yù)測，并對預(yù)測結(jié)果進(jìn)行平均，以更好地估計(jì)真實(shí)的輸出值。

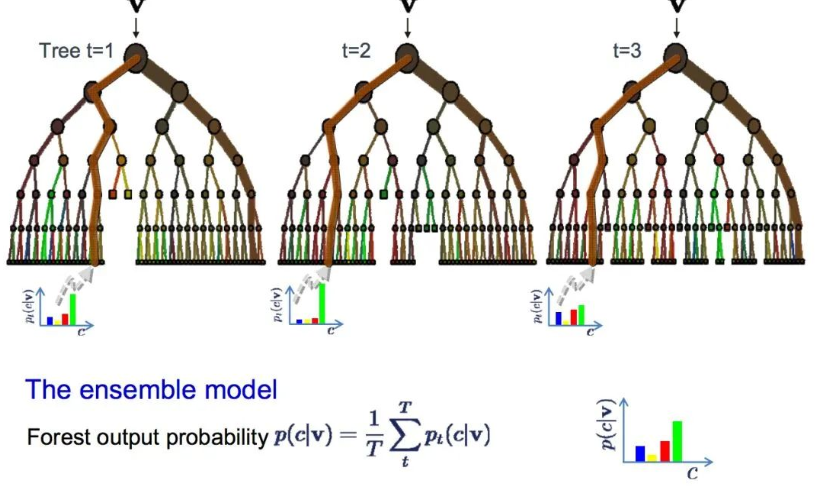
隨機(jī)森林是對決策樹的一種調(diào)整，相對于選擇最佳分割點(diǎn)，隨機(jī)森林通過引入隨機(jī)性來實(shí)現(xiàn)次優(yōu)分割。

因此，為每個(gè)數(shù)據(jù)樣本創(chuàng)建的模型之間的差異性會(huì)更大，但就自身意義來說依然準(zhǔn)確無誤。結(jié)合預(yù)測結(jié)果可以更好地估計(jì)正確的潛在輸出值。

如果你使用高方差算法(如決策樹)獲得良好結(jié)果，那么加上這個(gè)算法后效果會(huì)更好。

10、Boosting和AdaBoost

Boosting是一種從一些弱分類器中創(chuàng)建一個(gè)強(qiáng)分類器的集成技術(shù)。它先由訓(xùn)練數(shù)據(jù)構(gòu)建一個(gè)模型，然后創(chuàng)建第二個(gè)模型來嘗試糾正第一個(gè)模型的錯(cuò)誤。不斷添加模型，直到訓(xùn)練集完美預(yù)測或已經(jīng)添加到數(shù)量上限。

AdaBoost是為二分類開發(fā)的第一個(gè)真正成功的Boosting算法，同時(shí)也是理解Boosting的最佳起點(diǎn)。目前基于AdaBoost而構(gòu)建的算法中最著名的就是隨機(jī)梯度boosting。

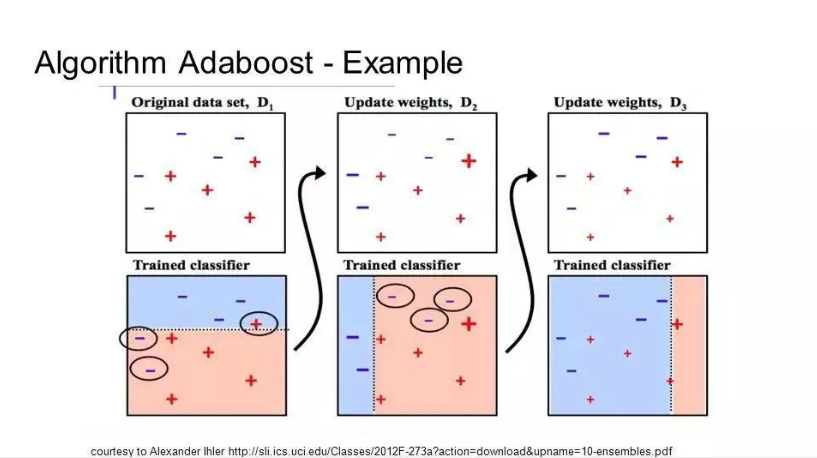
AdaBoost常與短決策樹一起使用。在創(chuàng)建第一棵樹之后，每個(gè)訓(xùn)練實(shí)例在樹上的性能都決定了下一棵樹需要在這個(gè)訓(xùn)練實(shí)例上投入多少關(guān)注。難以預(yù)測的訓(xùn)練數(shù)據(jù)會(huì)被賦予更多的權(quán)重，而易于預(yù)測的實(shí)例被賦予更少的權(quán)重。模型按順序依次創(chuàng)建，每個(gè)模型的更新都會(huì)影響序列中下一棵樹的學(xué)習(xí)效果。在建完所有樹之后，算法對新數(shù)據(jù)進(jìn)行預(yù)測，并且通過訓(xùn)練數(shù)據(jù)的準(zhǔn)確程度來加權(quán)每棵樹的性能。

因?yàn)樗惴O為注重錯(cuò)誤糾正，所以一個(gè)沒有異常值的整潔數(shù)據(jù)十分重要。

初學(xué)者在面對各種各樣的機(jī)器學(xué)習(xí)算法時(shí)提出的一個(gè)典型問題是“我應(yīng)該使用哪種算法?”問題的答案取決于許多因素，其中包括：

數(shù)據(jù)的大小，質(zhì)量和性質(zhì);

可用的計(jì)算時(shí)間;

任務(wù)的緊迫性;

你想要對數(shù)據(jù)做什么。

即使是一位經(jīng)驗(yàn)豐富的數(shù)據(jù)科學(xué)家，在嘗試不同的算法之前，也無法知道哪種算法會(huì)表現(xiàn)最好。雖然還有很多其他的機(jī)器學(xué)習(xí)算法，但這些算法是最受歡迎的算法。如果你是機(jī)器學(xué)習(xí)的新手，這是一個(gè)很好的學(xué)習(xí)起點(diǎn)。