8．2案例二：蒙特卡羅分析
   閱讀以下關于信息系統項目管理過程中風險管理和蒙特卡羅分析方面問題的敘述，回答問題1至問題3。
8.2.1案例場景
某公司實施CRM工程，實施過程中進行風險量化，其中的進度仿真采用蒙特卡羅分析，如圖8-2所示。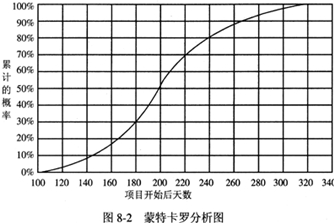

    需求調研階段，發現功能需求15個，非功能需求12個；需求復審階段，有10個用戶參與復審，所有復審者都有相同解釋的需求數目是24個。
    項目開發過程中，應用功能點法則，分解出的系統功能點有346開發過程中發現23個錯誤，提交后又發現3個錯誤。
    測試過程中，采用植入故障法估算程序中原有故障總數，人為植入的故障數是10個，經過一段時間的測試后發現的播種故障數是4個，在測試中又發現原有的故障數是2個。
    產品發布時，發布模塊總數是46個，和以前相比，變動6個模塊，新添加7個模塊，刪除6個模塊。
    【問題1】(8分)
    解釋案例中分析圖的含義，簡述進度仿真中，為什么不用傳統的數學分析技術(不超過250字)。
    【問題2】(8分)
    請用500字之內闡述項目質量管理中蒙特卡羅模擬方法的一般步驟。
    【問題3】(9分)
    根據案例中的數據，分別計算整體缺陷清除率、需求解釋一致性、程序中原有的故障數和軟件成熟度。
8.2.2案例分析
 【問題1】
    本題考查考生在進度仿真中對蒙特卡羅仿真結果進行分析的能力。要想回答好該題，考生需要了解蒙特卡羅曲線的實際意義。
    風險量化的目的是形成有關需要追逐的機遇和需要注意的威脅的清單，建立有關項目團隊有意識地接受或忽略的那些風險源和風險事件，以及誰決定這么做的文檔。進行風險量化的常用方法包括：期望的貨幣價值、統計綜合、風險仿真、決策樹等。其中風險仿真除了量化風險以外，還可以制定項目進度計劃。
    風險仿真使用系統的表示法或模型來分析系統的行為或性能。項目最常用的仿真形式，是使用項目網絡作為項目模型的進度仿真。大多數進度仿真是基于某種形式的蒙特卡羅(Monte Carlo)分析，該方法是一種模擬方法，通過多次“執行”目標項目，從而給出計算結果的統計分布，可以用來量化風險、計算在不同活動假設下的多個項目的持續時間。根據蒙特卡羅分析所得的結果，可以評估在不利條件下進度計劃的可行性；以及為了應付和減緩意外風險情況帶來的影響，要準備的應急/應對計劃；此外，該模擬結果還可以評估這些應急/應對計劃的可行性。
    該曲線利用蒙特卡羅分析描述項目的進度仿真，該S形曲線顯示了針對特
定日期，項目的累積概率。曲線的開始點表示項目開始的前100天為準備期，項目開始200天可以完成項目的50%,項目開始320天可以基本完成。該S曲線向左移動表示項目完成日期提前，但這樣有更高的風險；向右移動表示項目完成日期拖延，這樣風險會降低。
    任何大型或復雜的項目都應該進行進度仿真，傳統的數學分析技術，如關鍵路徑法(CPM)和項目評審技術(PERT)一等，都以最小值為基準，并且不計算路徑的交匯，這樣會低估項目的工期。
    【問題2】
    本題考查考生在進度仿真中運用蒙特卡羅模擬方法進行分析的能力。要想回答好該題，考生需要熟悉蒙特卡羅模擬方法的原理和使用步驟。
    蒙特卡羅模擬是一種隨機模擬方法。蒙特卡羅方法得名于歐洲著名賭城，摩納哥的蒙特卡羅。大概是因為賭博游戲與概率的內在聯系，第二次世界大戰時美國曼哈頓計劃中把這種方法稱為蒙特卡羅方法。在這之前，蒙特卡羅方法就已經存在。1777年，法國Buffon提出用投針實驗的方法求圓周率Π。這被認為是蒙特卡羅方法的起源。近年來，隨著計算機運算速度的提高，蒙特卡羅模擬得到了廣泛的運用。
    蒙特卡羅模擬的基本思想是人為地造出一種概率模型，使它的某些參數恰好重合于所需計算的量。又可以通過實驗，用統計方法求出這些參數的估值，把這些估值作為要求的量的近似值。
    在項目管理中，常常用到的隨機變量是與成本和進度有關的變量如價格、用時等。由于實際工作中可以獲得的數據量有限，它們往往是以離散型變量的形式出現的。例如，對于某種成本只知道最低價格、最高價格和最可能價格；對于某項活動的用時往往只知道最少用時、最多用時和最可能用時三個數據。經驗告訴我們，項目管理中的這些變量服從某些概率模型。現代統計數學則提供了把這些離散型的隨機分布轉換為預期的連續型分布的可能。可以利用計算機針對某種概率模型輕易進行數以千計、甚至數以萬計的模擬隨機抽樣。項目管理中蒙特卡羅模擬方法的一般步驟是：
    (1)對每一項活動，輸入最小、最大和最可能估計數據，并為其選擇一種合適的先驗分布模型。
    (2)計算機根據上述輸入，利用給定的某種規則，快速實施充分大量的隨機抽樣。
    (3)對隨機抽樣的數據進行必要的數學計算，求出結果。
    (4)對求出的結果進行統計學處理，求出最小值、最大值以及數學期望值和單位標準偏差。
    (5)根據求出的統計學處理數據，讓計算機自動生成概率分布曲線和累積概率曲線(通常是基于正態分布的概率累積S曲線)。
    (6)依據累積概率曲線進行項目風險分析。
    【問題3】
    本題考查考生在軟件開發中定量分析軟件質量的能力。要想回答好該題，考生需要熟悉軟件開發常用定量分析指標和計算方法。
    軟件的整體缺陷清除率指的是軟件產品開發過程中發現的缺陷數占軟件產品所有缺陷數的比率。設Dl為在開發過程(提交之前)中發現的所有缺陷數，D2為提交后發現的缺陷數，那么整體缺陷清除率就等于Dl/(Dl+D2)。一般而言，CMM等級越高，整體缺陷清除率也相應比較高。例如，美國的平均整體缺陷清除率目前只達到大約85%。而像AT&T, IBM,摩托羅拉和惠普這樣一些大公司的頂級項目，通過實施CMM,其缺陷清除率可以超過99%。
    對本題而言，D1=23，D2=3，則整體缺陷清除率為23/(23＋3)＝0.885=88.5％。
    軟件的需求解釋一致性指的是所有復審者都有相同解釋的需求數目和軟件中所有需求數目(功能需求和非功能需求之和)的比率。設Nui為所有復審者都有相同解釋的需求數目，Nf為功能需求的數目，Nnf為非功能需求數目，那么需求解釋一致性就等于Nui/ (Nf＋Nnf)。一般而言，如果軟件需求的模糊性越低，那么需求解釋一致性越接近1。
    對本題而言，Nui=24，Nf=15，Nnf= 12則整體需求解釋一致性為24/(15+12)=0.889= 88.9％。
    捕獲一再捕獲抽樣法利用測試前在程序中植入的故障數目來估算程序中原有的故障總數，該方法理論基礎是統計分析中的等概率事件原理，應用該方法的前提是要求對播種故障和原有故障同等對待。設Ns是在測試前人為地向程序中植入的故障數(稱播種故障)，ns是經過一段時間測試后發現的播種故障的數目，no是在測試中又發現的程序原有故障數，則程序中原有故障總數No的估算值為：No=(Ns/ns)no。
    對本題而言，Ns =10，ns = 4，no = 5則程序中原有的故障數No=(10/4)2 = 5
8.2.3參考答案
 【問題1】(8分)
    該曲線利用蒙特卡羅分析描述項目的進度仿真，該S形曲線顯示了針對特定日期，項目的累積概率。曲線的開始點表示項目開始的前100天為準備期，項目開始200天可以完成項目的50%,項目開始320天可以基本完成。該S曲線向左移動表示項目完成日期提前，但這樣有更高的風險；向右移動表示項目完成日期拖延，這樣風險會降低。
    任何大型或復雜的項目都應該進行進度仿真，傳統的數學分析技術，如關鍵路徑法(CPM)和項目評審技術(PERT)等，都以最小值為基準，并且不計算路徑的交匯，這樣會低估項目的工期。
    【問題2】(8分)
    蒙特卡羅模擬是一種有效的隨即模擬統計實驗方法，其基本思想是人為地造出一種概率模型，使它的某些參數恰好就是所需計算的量。又可以通過實驗，用統計方法求出這些參數的估值，把這些估值作為要求的量的近似值。
    項目管理中，經常用到的隨機變量大多是與成本和進度有關的變量，由于數據量有限，它們往往以離散性形式出現。有經驗可知，這些變量服從某些概率模型，利用蒙特卡羅方法結合這些概率模型就可以把那些離散分布轉換為連續分布。其一般步驟如下：
    (1)對每一項活動，輸入最小、最大和最可能估計數據，并為其選擇一種合適的先驗分布模型。
    (2)計算機根據上述輸入，利用給定的某種規則，快速實施充分大量的隨機抽樣。
    (3)對隨機抽樣的數據進行必要的數學計算，求出結果。
    (4)對求出的結果進行統計學處理，求出最小值、最大值以及數學期望值和單位標準偏差。-
    (5)根據求出的統計學處理數據，讓計算機自動生成概率分布曲線和累積概率曲線(通常是基于正態分布的概率累積S曲線)。
    (6)依據累積概率曲線進行項目風險分析。
    【問題3】(9分)
    整體缺陷清除率：23÷(23+3)=23÷26=0.885=88:5%；
    需求解釋一致性：．24÷(15+12)=24÷27=0.889=88.9%；
    程序中原有的故障數：(10÷4) × 2=5;
    軟件成熟度：[46-(6+7+6)]÷46=27÷46=0.587=58.7%。